2D

いいね 0

一覧

直角三角形	点で囲まれた多角形	三角形の内接円	三角形の外接円	正多角形の内接円	正多角形の外接円
２点間の距離と角度	２直線の交点と角度	原点を中心に回転	直交座標から極座標	極座標から直交座標	３点を通る円の中心

シンボル

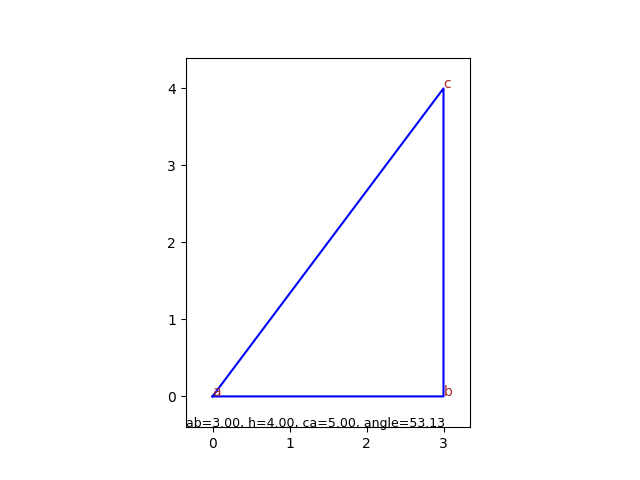
直角三角形 (RightTriangle)

辺ab、高さ、辺ca、aの角度のうち２つを入力して実行すると入力していない項目を算出して出力します

入力

ab

底辺の長さ

h

高さ

ca

斜辺の長さ

angle

角度

出力

out_ab

底辺の長さ（出力）

out_h

高さ（出力）

out_ca

斜辺の長さ（出力）

out_angle

角度（出力）

例

入力

ab

3.0

h

4.0

ca

angle

出力

out_ab

3.0

out_h

4.0

out_ca

5.0

out_angle

53.13

計算式

\begin{align} \theta =& angle*\frac{\pi}{180} \\ h =& ab \cdot tan\theta &= ca \cdot sin\theta \\ ab =& ca \cdot cos\theta \end{align}

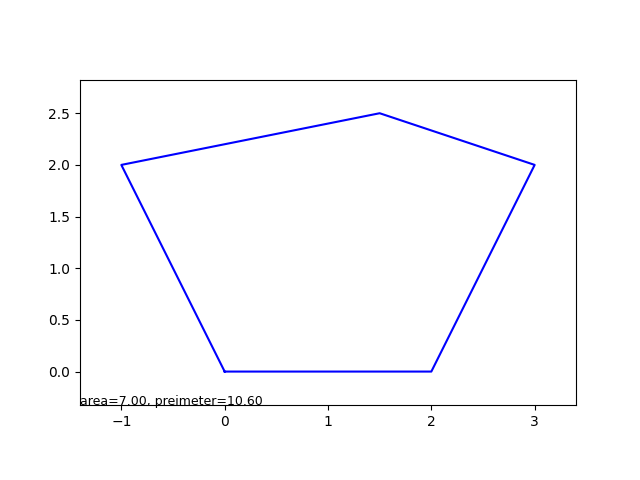
点で囲まれた多角形 (PolygonArea)

座標上の１０点までの点を繋げた多角形の面積と外周を出力します

入力

poits

点座標[x1,y1,x2,y2...]

n

点数

出力

area

面積

perimeter

外周

例

入力

poits

[0.0,0.0] [2.0,0.0] [3.0,2.0] [1.5,2.5] [-1.0,2.0]

n

5

出力

area

7.0

perimeter

10.60

計算式

\[ area = \frac{1}{2} \left|\sum_{j=1}^{n} (x_{j}-x_{j+1})*(y_{j}+y_{j+1})\right| \] \[ primeter = \sum_{j=1}^{n} \sqrt{(x_{j}-x_{j+1})^{2}+(y_{j}-y_{j+1})^{2}}\ \]

三角形の内接円 (TriangleInCircle)

３辺の長さを指定した三角形の内接円の半径と円の面積を出力します

入力

ab

辺１の長さ

bc

辺２の長さ

ca

辺３の長さ

出力

r

半径

area

面積

例

入力

ab

3.0

bc

4.0

ca

5.0

出力

r

1.0

area

3.14

計算式

\[ s = \frac{ab+bc+ca}{2} \] \[ r = \frac{\sqrt{s(s-ab)(s-bc)(s-ca)}}{s} \] \[ area = \pi r^{2} \]

三角形の外接円 (TriangleCircumCircle)

３辺の長さを指定した三角形の外接円の半径と円の面積を出力します

入力

ab

辺１の長さ

bc

辺２の長さ

ca

辺３の長さ

出力

r

半径

area

面積

例

入力

ab

3.0

bc

4.0

ca

5.0

出力

r

2.5

area

19.64

計算式

\[ s = \frac{ab+bc+ca}{2} \] \[ r = \frac{ab\cdot bc\cdot ca}{4\sqrt{s(s-ab)(s-bc)(s-ca)}} \] \[ area = \pi r^{2} \]

正多角形の内接円 (RegularPolygonInCircle)

辺の長さを指定した正多角形の内接円の半径と円の面積を出力します

入力

l

辺の長さ

n

辺の数

出力

r

半径

area

面積

例

入力

l

1.0

n

5

出力

r

0.69

area

1.49

計算式

\[ r = \frac{l}{2tan^{2}\frac{\pi}{n}} \] \[ area = \pi r^{2} \]

正多角形の外接円 (RegularPolygonCircumCircle)

辺の長さを指定した正多角形の外接円の半径と円の面積を出力します

入力

l

辺の長さ

n

辺の数

出力

r

半径

area

面積

例

入力

l

1.0

n

5

出力

r

0.85

area

2.27

計算式

\[ r = \frac{l}{2sin\frac{\pi}{n}} \] \[ area = \pi r^{2} \]

２点間の距離と角度 (LinearPtoP)

入力

p1

点1 [x,y]

p2

点2 [x,y]

出力

distance

距離

angle

角度

例

入力

p1

[-6.0,-3.0]

p2

[5.0,4.0]

出力

distance

13.038

angle

32.471

計算式

\[ distance = \sqrt{(p2_x-p1_x)^{2}+(p2_y-p1_y)^{2}} \] \[ angle = tan~{-1}\left( \frac{p2_y-p1_y}{p2_x-p1_x}\right) \]

計算式ではp1[0]を\(p1_x\)、p1[1]を\(p1_y\)と記述しています

２直線の交点と角度 (Intersection)

入力

Line1

線1 [始点x,始点y,終点x,終点y]

Line2

線2 [始点x,始点y,終点x,終点y]

出力

point

交点

angle

角度

例

入力

Line1

[-10, -7, 10, 3]

Line2

[-10, 13.4, 10, 10.6]

出力

point

[2,-1]

angle

-76.759

計算式

L1を一次関数(ax+b)に変換 \[ \begin{align} P1=&(L1[0,0],L1[0,1]) \\ P2=&(L1[1,0],L1[1,1]) \\ a1=&\frac{(P2_y-P1_y)}{(P2_x-P1_x)} \\ b1=&\frac{(P2_x*P1_y-P1_x*P2_y)}{(P2_x-P1_x)} \end{align} \] L2も同様に一次関数(ax+b)に変換して\(a2,b2\)を算出

L1,L2から \[ \begin{align} point_x = &\frac{(b2-b1)}{(a1-a2)} \\ point_y = &a1*point_x+b1 \\ angle=&tan^{-1}\left(\frac{a2-a1}{1+a1*a2} \right) \end{align} \]

原点を中心に回転 (PointRotate)

入力

p

点 [x,y]

angle

回転角度

出力

out_point

移動後の座標

例

入力

p

[4, 4]

angle

90.0

出力

out_point

[-4, 4]

計算式

\[ \begin{align} \theta =& angle\frac{\pi}{180} \\ outp_x =& p_x*cos\theta-p_y*sin\theta \\ outp_y =& p_x*sin\theta+p_y*cos\theta \\ \end{align} \]

計算式ではp[0]を\(p_x\)、p[1]を\(p_y\)と記述しています

直交座標から極座標 (PolarCoordinates)

直交座標から極座標へ変換

入力

p

点 [x,y]

出力

length

長さ

angle

角度

例

入力

p

[1.0,0.8]

出力

length

1.28

angle

38.66

計算式

\begin{align} length =& \sqrt{p_x^{2}+p_y^{2}} \\ \theta =& tan^{-1}\frac{p_y}{p_x} \\ angle =& \frac{180}{\pi}\theta \end{align}

計算式ではp[0]を\(p_x\)、p[1]を\(p_y\)と記述しています

極座標から直交座標 (CartesianCoordinates)

極座標から直交座標へ変換

入力

length

長さ

angle

角度

出力

p

点[x,y]

例

入力

length

2.0

angle

30.0

出力

p

[1.73,1.00]

計算式

\begin{align} \theta =& angle\frac{\pi}{180} \\ p_x =& length\cdot cos\theta \\ p_y =& length\cdot sin\theta \end{align}

計算式ではp[0]を\(p_x\)、p[1]を\(p_y\)と記述しています

平面の３点を通る円の中心と半径を求める (GetCenter2D)

平面の３点を通る円の中心と半径を求める

入力

点A

点A [x,y]

点B

点B [x,y]

点C

点C [x,y]

出力

p0

中心 [x,y]

r

半径

例

入力

点A

[-4, 2]

点B

[3, -1]

点C

[1, 6]

出力

p0

[0.128, 1.965]

r

4.128

計算式

\[ a = \begin{bmatrix} A_x & A_y & 1 \\ B_x & B_y & 1 \\ C_x & C_y & 1 \end{bmatrix} \] \[ bx = \begin{bmatrix} A_x^{2}+A_y^{2} & A_y & 1 \\ B_x^{2}+B_y^{2} & B_y & 1 \\ C_x^{2}+C_y^{2} & C_y & 1 \end{bmatrix} \] \[ by = \begin{bmatrix} A_x^{2}+A_y^{2} & A_x & 1 \\ B_x^{2}+B_y^{2} & B_x & 1 \\ C_x^{2}+C_y^{2} & C_x & 1 \end{bmatrix} \] \begin{align} p0_x=&-\left(\frac{bx}{2a}\right) \\ p0_y=&-\left(\frac{by}{2a}\right) \\ r=&\sqrt{(A_x-p0_x)^2+(A_y-p0_y)^2} \end{align}

計算式ではA[0]を\(A_x\)、A[1]を\(A_y\)と記述しています